sábado, 29 de noviembre de 2008
VENTA DISCOGRAFICA

En las primeras 10 semanas de cultivo de una planta, que medía 2.0 cm, se ha observado que su crecimiento es directamente proporcional al tiempo, viendo que en la primera semana ha pasado a medir 2.5 cm. Establecer una función lineal a fin que dé la altura de la planta en función del tiempo y representa gráficamente.
(Variable dependiente) (Variable independiente) (Ordenada en el origen)
Procedimiento: 1 semana. h= 0.5 *1 + 2= 2.5
2 semana. h= 0.5 *2 +2= 3 cm
3 semana. h= 0.5 *3 + 2= 3.5 cm
4 semana. h= 0.5 *4 + 2= 4 cm
5 semana. h= 0.5 *5 + 2= 4.5 cm
6 semana. h= 0.5 *6 + 2= 5 cm
7 semana. h= 0.5 * 7 +2= 5.5 cm
8 semana. h= 0.5 * 8 +2= 6 cm
9 semana. h= 0.5 * 9 +2= 6.5 cm
10 semana. h=0.5* 10 +2= 7 cm
A continuación se presenta la tabla y la grafica que representan a estos valores:
Temperatura altura
(Variable dependiente) (variable independiente) (ordenada en el origen)
Función lineal: t= -0.007 h + 15.6
Procedimiento: 1650 m: t= -0.007 h + 15.6 = 4.05 °c
1850 m : t= -0.007 h + 15.6 = 2.65 °c
2500 m: t= -0.007 h + 15.6= -1.9 °c
La siguiente tabla y la grafica repre
 sentan los valores anteriores:
sentan los valores anteriores:
1º B T/M
EQUIPO:- Adrian Martínez Lara
- José Alberto Jaramillo López
- Fernando Daniel Ojeda Chávez
- Omar Hassil Ramírez Rodríguez
- Luis enrique Gonzales Vásquez
COMPAÑIA DE AUTOMOVILES
Graficas lineales
Una compañía de automóviles al probar unos de sus nuevos modelos en relación con distancia de frenado bajo cierta velocidad obtuvo la siguiente tabla y una grafica nos muestra la velocidad en kilómetros sobre la distancia de frenado en metros dándonos así una grafica lineal.

EQUIPO DE MAYRA ALEJANDRA PEÑA LOPEZ
viernes, 28 de noviembre de 2008
Gráficas lineales
Con base en la tabla anterior podemos construir una grafica considerando que la variación viene dada por línea recta, para cualquier x, la relación que se induce es
Esta fórmula nos permite dibujar una gráfica.
Hemos logrado escribir una variable independiente y en términos de una variable independiente x, lo que permite calcular la variable y para cualquier valor de la variable x.

MEGACABLE
Equipo:
1-Zuleima Berenice Avelar Ruelas
2-Oscar Raúl Moreno García
3-Miriam Anabel Marin Duran

Y la respuesta al problema se resuelve asi: 4340 (pagos) + 250 (suscripcion) =4590
R=4590
TEMPERATURA
1-Zuleima Berenice Avelar Ruelas
2-Oscar Raúl Moreno García
3-Miriam Anabel Marin Duran
Bien, pues aqui les dejo el primero de los problemas de funcion lineal,
Y despues lo graficaremos en una grafica lineal, la cual quedara de la siguiente manera:

jueves, 27 de noviembre de 2008
Una mujer recibió:
El recibo de la TV por cable que es de $590.00 y el adeudo incrementa un 28% por mes de retraso, si se retraso 8 meses;
¿Cuánto pagara pasado ese tiempo?
| Meses de atraso | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| $ pago | $590 | $752.50 | $915 | $1077.50 | $1240 | $1402.50 | $1565 | $1727.50 | $1890 |
R= En 8 meses pagara $1,890.00
En enero volvió a llegar el recibo, esta vez con el 35% de aumento en el adeudo
¿Cuánto pagara en 6 meses?
100 – 590
35 – 206.5
| Meses de atraso | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| $ pago | $90 | $796.50 | $1003 | $1209.50 | 1416 | 1622.5 | 1829 |
R= En 6 meses pagara $1,829
Grafica con el 28%
Grafica con el 35%
Para entregar en el aula el día 1 de diciembre
- Reducir las siguientes expresiones:

d)

- Realiza las siguientes operaciones:
- Encontrar el valor de la incógnita en las siguientes ecuaciones:
Reducción de terminos semejantes
lo prometido es deuda, hay que realizar ejercicios para practicar lo que vimos en el aula ahora que estamos recordando conceptos básicos de Álgebra.
Primero recordemos lo que son los términos y cada una de sus partes, para ello les recomiendo visiten la página http://publab03.coseac.unam.mx/objetos/operacionesmp.html, si no creen que sea necesario revisar la teoría, entonces vayan directo a la página http://publab03.coseac.unam.mx/objetos/cuestionario1.html, en ella podrán realizar la primer actividad y evaluar ustedes mismos sus resultados.
En segundo lugar hay que recordar lo que son los términos semejantes la teoría pueden encontrarla en http://publab03.coseac.unam.mx/objetos/termsemj.html, ahí vienen unas animaciones que ilustran los términos semejantes de forma similar a como lo vimos en clase. Practiquen como reducir términos semejantes en la página http://publab03.coseac.unam.mx/objetos/cuestionario2.html
pueden también ver si los resultados que obtuvieron son correctos dando click en el botón que dice "verificar respuestas".
Otros ejercicios que pueden hacer para practicar mas son los que estan en http://publab03.coseac.unam.mx/objetos/cuestionario3.html.
Luego, para practicar la resolción de ecuaciones de primer grado realicen los ejercicios que están en la página http://www.juntadeandalucia.es/averroes/html/adjuntos/2008/05/09/0003/recurso/tests/primerbasico/prbas0101.htm, en esta página también pueden verificar sus resultados y hacer ustedes una autoevaluación.
Ahora si, ¡a practicar!
Practica de Física
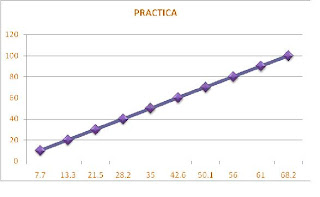
En la preparatoria de Tonalá el maestro de física les pidió a los alumnos de 1ºB que realizaran una práctica en el patio trasero, la práctica consistía en que cada alumno debía de trotar sobre una línea recta de 100 metros en la cual debería de identificar cuantos segundos duraba del 0m a 10m, de 10m a 20m, de 20m a 30m etc. etc.
En la siguiente tabla se muestran los resultados.
En la siguiente gráfica de muestran los resultados. En el eje horizontal se muestran los segundos y en el vertical los metros.
Ejemplo de Lucy Sahagún
Gráfica de la maestra con los datos de Lucy:
miércoles, 26 de noviembre de 2008
Fernando Hitt
Capítulo 5 “funciones lineales en contexto”.
Ejemplo 5.1
Queremos fabricar un recipiente, en forma de cilindro y nos interesa ponerle marcas para saber el volumen del líquido que puede contener. Supongamos que tenemos el recipiente con base circular (véase fig. 5.1) y lo estamos llenando con un líquido. El radio de la base es r = 5cm y la altura del recipiente es h = 12cm, ¿Cuál será el volumen del líquido en ese recipiente en tanto varía la altura? Figura 5.1

r= 5cm Plantearemos la pregunta de otra manera: ¿Cómo varía el volumen del líquido en función de su altura? H dicho así, tendríamos que encontrar una expresión algebraica de tal forma que relacione la altura (variable independiente) h con el volumen (variable dependiente).
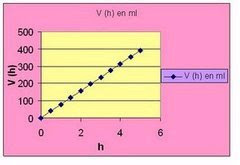
El volumen de un cilindro se calcula multiplicando su base por la altura. En nuestro caso el área de la base circular del recipiente es π r2. Puesto que la variable independiente h representa la altura conforme el líquido va subiendo, el volumen estaría dado por (π r2) 0 h; es decir, el volumen V en términos de la altura lo podemos escribir así: V (h)=( π r2.0 h. V (h) – (28 π)0 h). Para diferentes valores de h tomando una aproximación de π, por ejemplo 3,4, podemos generar una tabla y su correspondiente gráfica (véase figura 5.2).

También utilizando la fórmula y haciendo variar h entre OyH=12cm, se obtiene la gráfica de la figura 5.3. A partir de esta gráfica podemos calcular el volumen del líquido señalando cualquier altura entre 0 y 12 cm. Podríamos con ello para diferentes valores de la altura, marcar en el recipiente los valores correspondientes del volumen. Figura 5.3


Integrantes:
Maria Guadalupe García Reyes
Maria Isabel Ceceña Maestro.
martes, 25 de noviembre de 2008
Problema del recibo telmex
http://www.x.edu.uy/lineal.htm
La renta de una línea de teléfono Telmex mas Internet al mes es de un pago fijo de $338.26 con un límite de 100 llamadas locales sin ningún costo, el costo de una llamada a larga distancia por un minuto es de $2.00.
Con los datos anteriores completa la siguiente tabla:
1) 0*2+338.26=338.26
2) 5*2+338.26=348.26
3) 15*2+338.26=368.26
4) 25*2+338.26=388.26
5) 38*2+338.26=414.26
6) 45*2+338.26=428.26
7) 56*2+338.26=450.26
8) 62*2+338.26=462.26
9) 79*2+338.26=496.26
10) 83*2+338.26=504.26
Problema de la comisión Federal de electricidad
“Problema de la comisión federal de electricidad”
Este problema lo hicimos con base a la formula y=mx+b de una función lineal ya que esta es un polinomio de primer grado.
http://www.x.edu.uy/lineal.htm
Los consumos de algún servicio básico en este caso la electricidad tienen un medidor en el cual presentan un cargo fijo ya sea por emisión de boleta o por arriendo de algún tipo de medidor, con esta información se pueden presenta una constante que puede ser utilizada con una función lineal.
La factura de la electricidad incluye un monto fijo de $125.00 (costo de producción) que se cobre haya o no consumo una cantidad $2.170 (dos punto uno siete cero pesos) por cada kilowatt-hora. (Según la CFE http://www.cfe.gob.mx/es/InformacionAlCliente/conocetutarifa/acuerdos/2005/acuerdo20050121.htm )
Con los datos anteriores completa la siguiente tabla:
 Procedimiento: FORMULA: y=mx+b
Procedimiento: FORMULA: y=mx+b cobro mensual= KW * 2.170 + 125
1) 0*2.170+125=125
2) 5*2.170+125=135.85
3) 25*2.170+125=179.25
4) 45*2.170+125=222.65
5) 70*2.170+125=276.9
6) 100*2.170+125=342
7) 125*2.170+125=396.25
8) 155*2.170+125=461.35
9) 200*2.170+125=559
10) 230*2.170+125=624.1

Integrantes: Cristina Rojo, Cristian Pimienta, Erika Sarai Sánchez.
FUNCIONES LINEALES
FERNANDO HITT
TEMA: Funciones Lineales en Contexto
Ejemplo 5.2 Pág.81-83
Un diario francés publicó en su edición dominical la información que se muestra en la figura 5.4 y en la tabla 5.1 acerca de la nueva ley sobre infracciones por manejar con cierto grado de alcohol en la sangre.
Figura 5.4
Buscando la información al respecto encontramos lo que se muestra en la tabla 5.2, que se limita a una relación de cierta cantidad de alcohol en la sangre.
Según parece, la regla que rige al fenómeno de eliminación de alcohol esta dada por una función lineal. Tomemos una desición, tracemos la línea recta para modelar el fenómeno (vea la figura 5.5) tomemos la ley emitida en Francia en 1994 sobre la restricción de no manejar si se sobrepasa 0.7 g/l de alcohol en la sangre. Tracemos la línea horizontal que pasa por 0.7 en la misma gráfica.
De la gráfica de la figura5.5 podemos saber el tiempo mínimo que unas persona tiene que esperar para poder manejar sin cometer infracción, la cual es 2 horas con 57 minutos. Si quisiéramos una formula que nos ayudara a calcular con presición el grado de alcohol en la sangre en cualquier momento, después de tomar 5 cervezas, podríamos usar la semejanza de triángulos para obtener la relación entre variables, lo daría

**"RELACIONES LINEALES Y LA TARJETA DE DEBITO"**
Una de las mejores maneras de llegar al tipo de dependencia funcional que existe entre dos variables, es dibujar una gráfica de las variables en un sistema cartesiano de coordenadas. Los valores experimentales de la variable independiente se marcan en el eje horizontal (abscisa) y la variable dependiente se marca sobre el eje vertical (ordenada). Después de analizar si la tendencia de los puntos en el gráfico se ajusta a una línea recta o a una curva, se puede determinar la naturaleza de la función que relaciona las variables, especialmente si esta función tiene una forma sencilla.
La construcción de gráficas debe iniciarse con la elaboración de una tabla de los datos, los cuales pueden disponerse en columnas o en filas. Toda tabla debe llevar un titulo explicativo que indique el significado de los datos y la forma como fueron obtenidos.
Uno de los requisitos más importantes de un gráfico, es la elección de escalas para los dos ejes de coordenadas. Debe tenerse presente que un gráfico de datos de laboratorio carece de significado si no se identifica cada eje con la cantidad medida y las unidades utilizadas para medir. Algunas sugerencias para la elaboración de gráficas se presentan a continuación:
• Poner un título al gráfico que sea conciso y claro.• Seleccionar una escala que facilite la representación y la lectura. Se deben elegir escalas que puedan subdividirse fácilmente. Valores recomendables son 1, 2, 5 y 10 unidades por escala de división. No se recomiendan escalas como 3, 7, 6, 9 debido a que hacen difícil la localización y la lectura de los valores en el gráfico. Procurar que el gráfico ocupe la mayor parte de hoja de papel.• No es necesario representar ambas cantidades en la misma escala, ni que comience en cero.• Representar todos los datos observados. Demarcar claramente los puntos experimentales con un punto dentro de un pequeño círculo, o dentro de un triángulo, o algún otro símbolo semejante. Unir el mayor número de puntos con una curva suave, de modo que aquellos que queden por fuera de la curva queden igualmente repartidos por encima y por debajo.
**RELACIONES LINEALES**
una recta y la forma general de la función es como sigue:
y = mx + b (1)
en donde m es la pendiente de la línea y b su intercepto con el eje y, es decir el valor de y cuando x = 0. Por ejemplo, en la fórmula para convertir grados Fahrenheit (ºF) a grados centígrados (ºC):
ºF = 9/5 ºC + 32 (2)
9/5 es la pendiente de la línea y 32 es el intercepto con y cuando x = 0. Esta ecuación nos permite convertir grados Fahrenheit a grados centígrados o viceversa. En este caso se dice que la escala Fahrenheit está relacionada en forma lineal con la escala centígrada, aunque no son directamente proporcionales.
Si el gráfico de datos aparece sobre el papel como una recta que pasa por el origen, entonces su ecuación es de la forma y = mx, entonces y varía en forma directamente proporcional a x.
Se midió la solubilidad del KCl en agua a diferentes temperaturas, expresada como g KCl/100 g H2O, y se obtuvieron los siguientes datos:
S (%)
30
31
35
36
40
42
45
49
51
T (ºC)
10
20
30
40
50
60
70
80
90
Los datos aparecen graficados a continuación:

(3)

= T (°C)
y = S (%)
xy
x2
10
30
300
100
20
31
620
400
30
35
1050
900
40
36
1440
1600
50
40
2000
2500
60
42
2520
3600
70
45
3150
4900
80
49
3920
6400
90
51
4590
8100
S x = 450(S x)2 = 202500
S y = 359
S xy = 19590
S x 2 = 28500
Con n = 9, se tiene que . Análogamente, b = 26.2.
La función que representa la relación entre la solubilidad y la temperatura es, por lo tanto:
S = 0.273 T + 26.2.
Alexa acaba de tramitar una tarjete de debito, al ella le hacen un descuento del 10% en su primera compra. Al dia siguiente fue a la tienda y tenian una promoción de pagar a 15 mensualidades con un interes fijo del 3%. El producto que le gusto a ella tenia el costo de $189.90.¿cuanto va a pagar en total?
189,9
100
189.90 10
4, 100, 5, 9, 5, 17, 5, 38
1899
?
10
1899
2, 70, 7, 4, 3, 17, 8, 0
100
18,99
R= 170.91
Ahora, obten el 3% que es el interes fijo.
170,91
100
3, 5, 13, 28, 3, 69, 14, 18
4, 100, 13, 32, 5, 12, 14, 8
170.91 3 512.73
?
3%
512,73
2, 68, 15, 8, 3, 17, 15, 25
100
5,1273
R= 3% = 5.1273
Muy bien ahora con esos datos vas a contestar lo siguiente utilizando es formula: M=C/m+I ;esto quiere decir (M) monto a pagar cada mes, ( C ) costo del articulo,(m) mensualidades, (I) interes a pagar. ¿cuanto tiene que pagar cada mes alexa?
mensualidades
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
monto a pagar
170,91
176,0373
181,1646
186,2919
191,4192
196,5465
201,6738
206,8011
211,9284
217,0557
222,183
227,3103
232,4376
237,5649
242,6922
interes
5,1273
5,1273
5,1273
5,1273
5,1273
5,1273
5,1273
5,1273
5,1273
5,1273
5,1273
5,1273
5,1273
5,1273
5,1273
Ahora graficala para comprobar si es una función lineal.
- Katia Valdez. # de Lista: 43.
- Flor Zúñiga. # de lista: 47.
- Guadalupe Benitez. # de Lista: 4.
- Ángel Rodríguez. # de Lista: 35.
"La depreciación"
Cuando las empresas adquieren equipo, los contadores por lo general asignan el costo del artículo sobre el periodo que este se va a emplear. Por ejemplo, a un camión cuyo costo sea de $ 600 000 y una vida útil de cinco años, los contadores podrían asignarle $ 24 000 al año como costo de adquisición. El costo asignado a cualquier periodo se le denomina depreciación. Los contadores conservan registrados del activo principal y su valor corriente o “de libro”. Asi, el valor del camión podría aparecer en los estados de contabilidad como $600 000 al principio (600 000 – 24 000) = $ 576 000 al año siguiente. Etc. La depreciación puede considerarse también como el monto en el que se ha disminuido el valor en libros de un activo.
Un caso especial es la depreciación lineal, aquella en la que la tasa de depreciación se mantiene constante. En este caso del camión, si V es el valor en libros y t es el tiempo en años, entonces:
V= Costo de Adquisición – Depreciación
V= 6000 000 – 240 000 t
Ahora a estas distintas cantidades se les resta la depreciación:
A continuación se muestra la gráfica de esta función lineal.
Equipo:
Virginia Delgadillo Alcaraz.
Andrea Berenice Alvizu Silva.
Cinthya Suárez de la Rosa.
Cecilia Belén Garcia Suárez.
"La alberca"
Supongamos que en un centro deportivo hay una alberca como la siguiente.

Queremos saber el volumen del agua contenida y la variación del volumen conforme se va llenando. Entonces, necesitamos calcular el volumen del agua en términos de la altura.
Transformaremos nuestro dibujo en uno que nos permita matematizar la situación propuesta.
El volumen, en términos de la altura, estará dado por el volumen del primer paralelepípedo, más el volumen del segundo paralelepípedo. Entonces, el volumen en términos de la altura será:
Virginia Delgadillo Alcaraz.
Andrea Berenice Alvizu Silva.
Cinthya Suárez de la Rosa.
Cecilia Belén Garcia Suárez.

Fernando Hitt
Capítulo 5 “funciones lineales en contexto”.
Ejemplo 5.1
Queremos fabricar un recipiente, en forma de cilindro y nos interesa ponerle marcas para saber el volumen del líquido que puede contener. Supongamos que tenemos el recipiente con base circular (véase fig. 5.1) y lo estamos llenando con un líquido. El radio de la base es r = 5cm y la altura del recipiente es h = 12cm, ¿Cuál será el volumen del líquido en ese recipiente en tanto varía la altura?
Figura 5.1
función de su altura? dicho así, tendríamos que encontrar una expresión algebraica de tal forma que relacione la altura (variable independiente)con el volumen (variable dependiente).
El volumen de un cilindro se calcula multiplicando su base por la altura. En nuestro caso el área de la base circular del recipiente es π r2. Puesto que la variable independiente h representa la altura conforme el líquido va subiendo, el volumen estaría dado por (π r2) 0 h; es decir, el volumen V en términos de la altura lo podemos escribir así: V (h)=( π r2.0 h. V (h) – (28 π)0 h). Para diferentes valores de h tomando una aproximación de π, por ejemplo 3,4, podemos generar una tabla y su correspondiente gráfica (véase figura 5.2).
h en cm V (h) en ml

0 y 12 cm. Podríamos con ello para diferentes valores de la altura, marcar en el recipiente los valores correspondientes del volumen.
Figura 5.3